విషయము

• దశలు
• సలహా

మీరు గణిత శాస్త్రజ్ఞుడు లేదా గ్రాఫిక్ ప్రోగ్రామర్ అయితే, మీరు ఇచ్చిన రెండు వెక్టర్ల మధ్య కోణాన్ని కనుగొనవలసి ఉంటుంది. ఈ వ్యాసంలో, వికీ ఎలా చేయాలో మీకు చూపుతుంది.

దశలు

2 యొక్క పార్ట్ 1: రెండు వెక్టర్స్ మధ్య కోణాన్ని కనుగొనండి

1. 

   వెక్టర్ నిర్వచనం. మీ వద్ద ఉన్న రెండు వెక్టర్లకు సంబంధించిన మొత్తం సమాచారాన్ని రాయండి. మీరు వారి డైమెన్షనల్ కోఆర్డినేట్స్ యొక్క పేర్కొన్న పారామితులను మాత్రమే కలిగి ఉన్నారని అనుకుందాం (భాగాలు అని కూడా పిలుస్తారు). వెక్టర్ యొక్క పొడవు (పరిమాణం) మీకు ఇప్పటికే తెలిస్తే, మీరు క్రింద ఉన్న కొన్ని దశలను దాటవేయవచ్చు.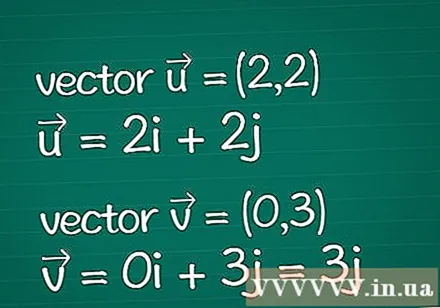
   • ఉదాహరణ: రెండు డైమెన్షనల్ వెక్టర్ = (2,2) మరియు రెండు డైమెన్షనల్ వెక్టర్ = (0,3). వాటిని = 2 అని కూడా వ్రాయవచ్చుi + 2j మరియు = 0i + 3j = 3j.
   • ఈ వ్యాసంలోని ఉదాహరణలో రెండు డైమెన్షనల్ వెక్టర్స్ ఉపయోగించినప్పటికీ, కింది సూచనలు ఎన్ని కొలతలు ఉన్న వెక్టర్లకు వర్తిస్తాయి.

2. 

   
   
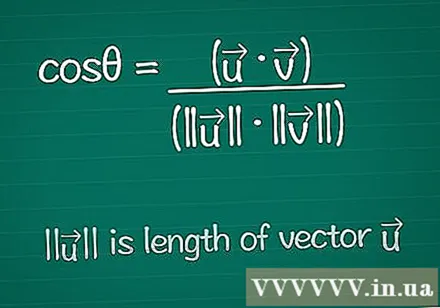
   కొసైన్ సూత్రాన్ని వ్రాయండి. రెండు వెక్టర్ల మధ్య the కోణాన్ని కనుగొనడానికి, ఆ కోణం కోసం కొసైన్‌ను కనుగొనే సూత్రంతో ప్రారంభిస్తాము. మీరు ఈ సూత్రం గురించి క్రింద తెలుసుకోవచ్చు లేదా దీన్ని ఇలా వ్రాసుకోండి:
   • cosθ = (•) / (|||| ||||)
   • |||| అంటే "వెక్టర్ యొక్క పొడవు".
   • Ve అనేది రెండు వెక్టర్స్ యొక్క స్కేలార్ ఉత్పత్తి - ఇది క్రింద వివరించబడుతుంది.

3. 

   
   
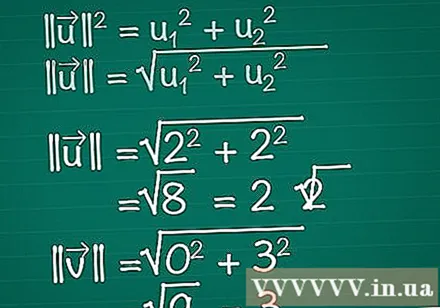
   ప్రతి వెక్టర్ యొక్క పొడవును లెక్కించండి. ఒక కుడి త్రిభుజం వెక్టర్ యొక్క x, y భాగాలు మరియు వెక్టర్‌తో తయారవుతుందని g హించుకోండి. వెక్టర్ త్రిభుజం యొక్క హైపోటెన్యూస్‌ను ఏర్పరుస్తుంది, కాబట్టి దాని పొడవును కనుగొనడానికి మేము పైథాగరియన్ సిద్ధాంతాన్ని ఉపయోగిస్తాము. వాస్తవానికి, ఈ సూత్రాన్ని ఎన్ని కొలతలు కలిగిన వెక్టర్‌కు సులభంగా విస్తరించవచ్చు.
   • || యు || = యు₁ + యు₂. వెక్టార్‌లో రెండు కంటే ఎక్కువ అంశాలు ఉంటే, మీరు + u ని జోడించడం అవసరం₃ + యు₄ +...
   • అందువల్ల, రెండు డైమెన్షనల్ వెక్టర్ కోసం, || యు || = √ (యు₁ + యు₂).
   • ఈ ఉదాహరణలో, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
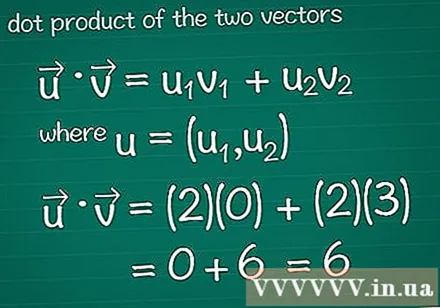
   రెండు వెక్టర్స్ యొక్క స్కేలార్ ఉత్పత్తిని లెక్కించండి. బహుశా మీరు వెక్టర్ గుణకారం యొక్క పద్ధతిని నేర్చుకున్నారు, దీనిని కూడా పిలుస్తారు స్కేలార్ ఇది. వాటి కూర్పుకు సంబంధించి స్కేలార్ ఉత్పత్తిని లెక్కించడానికి, ప్రతి దిశలోని పదార్థాలను కలిపి గుణించి, ఆపై మొత్తం ఫలితాన్ని జోడించండి.
   • గ్రాఫిక్స్ ప్రోగ్రామ్ కోసం, దయచేసి మరింత చదవడానికి ముందు చిట్కాలను చూడండి.
   • గణితంలో • = యు₁v₁ + యు₂v₂, ఎక్కడ, u = (యు₁, యు₂). వెక్టర్ రెండు కంటే ఎక్కువ మూలకాలను కలిగి ఉంటే, + u ని జోడించండి₃v₃ + యు₄v₄...
   • ఈ ఉదాహరణలో, • = u₁v₁ + యు₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. ఇది వెక్టర్ మరియు వెక్టర్ యొక్క స్కేలార్ ఉత్పత్తి.

5. 

   పొందిన ఫలితాలను సూత్రంలో ఉంచండి. Cosθ = (•) / (|||| || ||) అని గుర్తుంచుకోండి. స్కేలార్ ఉత్పత్తి మరియు ప్రతి వెక్టర్ యొక్క పొడవు రెండూ ఇప్పుడు మనకు తెలుసు. కోణం యొక్క కొసైన్‌ను లెక్కించడానికి వీటిని సూత్రంలో నమోదు చేయండి.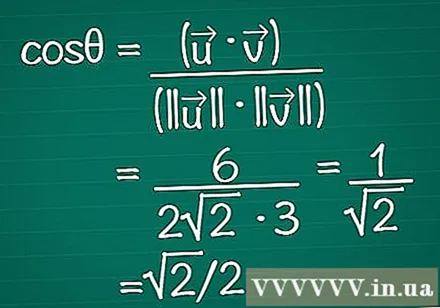
   • మా ఉదాహరణలో, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   దాని కొసైన్ ఆధారంగా కోణాన్ని కనుగొనండి. తెలిసిన కాస్ విలువ నుండి find ను కనుగొనడానికి మీరు కాలిక్యులేటర్‌లో ఆర్కోస్ లేదా కాస్ ఫంక్షన్‌ను ఉపయోగించవచ్చు. కొన్ని ఫలితాలతో, మీరు యూనిట్ సర్కిల్ ఆధారంగా కోణాన్ని కనుగొనవచ్చు.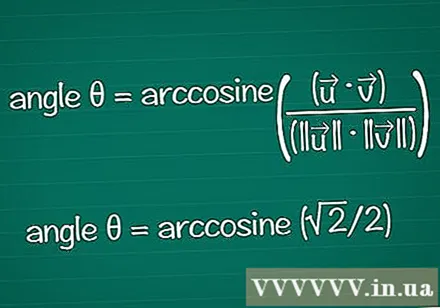
   • ఉదాహరణలో, cosθ = √2 / 2. కోణాన్ని కనుగొనడానికి మీ కాలిక్యులేటర్‌లో "ఆర్కోస్ (√2 / 2)" ను నమోదు చేయండి. లేదా, మీరు cosθ = √2 / 2 స్థానంలో యూనిట్ సర్కిల్‌లో కోణం find ను కనుగొనవచ్చు. ఇది నిజం θ = /₄ లేదా 45º.
   • అన్నింటినీ కలిపి, చివరి సూత్రం: కోణం θ = ఆర్కోసిన్ ((•) / (|||| || ||))
   ప్రకటన

2 యొక్క 2 వ భాగం: కోణ సూత్రం యొక్క నిర్ధారణ

1. 

   సూత్రం యొక్క ఉద్దేశ్యాన్ని అర్థం చేసుకోండి. ఈ సూత్రం ఇప్పటికే ఉన్న నిబంధనల నుండి తీసుకోబడలేదు. బదులుగా, ఇది స్కేలార్ ఉత్పత్తి యొక్క నిర్వచనం మరియు రెండు వెక్టర్స్ మధ్య కోణంగా ఏర్పడుతుంది. అయినప్పటికీ, ఇది ఏకపక్ష నిర్ణయం కాదు. ప్రాథమిక జ్యామితికి తిరిగి వెళితే, ఈ సూత్రం సహజమైన మరియు ఉపయోగకరమైన నిర్వచనాలను ఎందుకు అందిస్తుందో మనం అర్థం చేసుకోవచ్చు.
   • దిగువ ఉదాహరణలు రెండు డైమెన్షనల్ వెక్టర్లను ఉపయోగిస్తాయి ఎందుకంటే అవి అర్థం చేసుకోవడానికి సులభమైనవి మరియు సరళమైనవి. త్రిమితీయ లేదా అంతకంటే ఎక్కువ వెక్టర్స్ దాదాపు సారూప్య సాధారణ సూత్రాల ద్వారా నిర్వచించబడిన లక్షణాలను కలిగి ఉంటాయి.

2. 

   కొసైన్ సిద్ధాంతాన్ని సమీక్షించండి. A మరియు b వైపుల మధ్య angle కోణంతో సాధారణ త్రిభుజాన్ని పరిగణించండి, ఎదురుగా c. కొసిన్ సిద్ధాంతం c = a + b -2ab అని పేర్కొందిcos(). ఈ ఫలితం ప్రాథమిక జ్యామితి నుండి చాలా సరళంగా తీసుకోబడింది.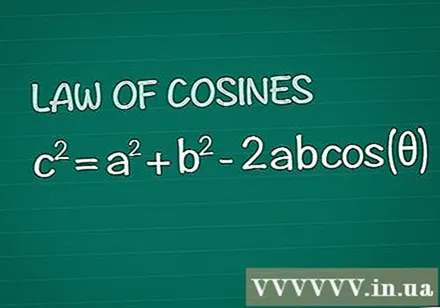

3. 

   రెండు వెక్టర్లను కనెక్ట్ చేయండి, త్రిభుజం ఏర్పడుతుంది. కాగితం, వెక్టర్స్ మరియు వెక్టర్స్‌పై రెండు-డైమెన్షనల్ వెక్టర్స్‌ను గీయండి, వాటి మధ్య కోణం ఉంటుంది. త్రిభుజాన్ని సృష్టించడానికి ఈ రెండింటి మధ్య మూడవ వెక్టర్ గీయండి. మరో మాటలో చెప్పాలంటే, + = వంటి వెక్టర్‌ను గీయండి. వెక్టర్ = -.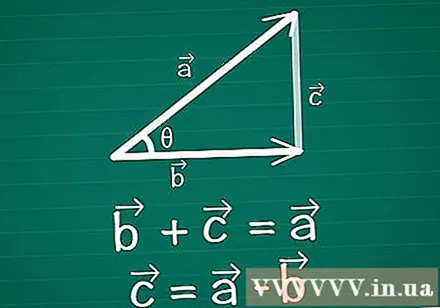

4. 

   ఈ త్రిభుజం కోసం కొసైన్ సిద్ధాంతాన్ని వ్రాయండి. మా "వెక్టర్ త్రిభుజం" యొక్క సైడ్ పొడవును కొసైన్ సిద్ధాంతంలోకి మార్చండి:
   • || (అ - బి) || = || అ || + || బి || - 2 || అ || || బి ||cos(θ)

5. 

   స్కేలార్ ఉత్పత్తితో తిరిగి వ్రాయండి. గుర్తుంచుకోండి, స్కేలార్ ఉత్పత్తి అనేది ఒక వెక్టార్ యొక్క చిత్రం. వెక్టర్ యొక్క స్కేలార్ ఉత్పత్తికి ప్రొజెక్షన్ అవసరం లేదు, ఎందుకంటే ఇక్కడ, దిశలో తేడా లేదు. అంటే • = || అ ||. దీనిని ఉపయోగించి, మేము సమీకరణాన్ని తిరిగి వ్రాస్తాము:
   • (-) • (-) = • + • - 2 || అ || || బి ||cos(θ)

6. 

   అదే సూత్రాన్ని విజయవంతంగా తిరిగి వ్రాసారు. ఫార్ములా యొక్క ఎడమ వైపు విస్తరించండి, ఆపై కోణాలను కనుగొనడానికి ఉపయోగించే సూత్రాన్ని పొందడానికి సరళీకృతం చేయండి.
   • • - • - • + • = • + • - 2 || అ || || బి ||cos(θ)
   • - • - • = -2 || అ || || బి ||cos(θ)
   • -2 (•) = -2 || అ || || బి ||cos(θ)
   • • = || అ || || బి ||cos(θ)
   ప్రకటన

సలహా

• విలువలను మార్చడానికి మరియు సమస్యను త్వరగా పరిష్కరించడానికి, ఏదైనా రెండు-డైమెన్షనల్ వెక్టర్స్ కోసం ఈ సూత్రాన్ని ఉపయోగించండి: cosθ = (u₁ • v₁ + యు₂ • v₂) / ((యు₁ • u₂) • √ (వి₁ • v₂)).
• మీరు కంప్యూటర్ గ్రాఫిక్స్ సాఫ్ట్‌వేర్‌తో పనిచేస్తుంటే, మీరు వెక్టర్ యొక్క కొలతలు మాత్రమే పట్టించుకోవాలి మరియు వాటి పొడవు గురించి కాదు. సమీకరణాన్ని తగ్గించడానికి మరియు మీ ప్రోగ్రామ్‌ను వేగవంతం చేయడానికి క్రింది దశలను ఉపయోగించండి:
  • ప్రతి వెక్టర్‌ను సాధారణీకరించండి, తద్వారా అవి 1. దీన్ని చేయడానికి, వెక్టర్ యొక్క ప్రతి భాగాలను దాని పొడవుతో విభజించండి.
  • అసలు వెక్టార్‌కు బదులుగా స్కేలార్ యొక్క సాధారణీకరించిన ఉత్పత్తిని పొందండి.
  • పొడవు 1 కాబట్టి, మేము సమీకరణం నుండి పొడవు మూలకాలను మినహాయించవచ్చు. చివరగా, పొందిన కోణ సమీకరణం ఆర్కోస్ (•).
• కొసైన్ సూత్రం ఆధారంగా, కోణం అక్యూట్ లేదా అస్పష్టంగా ఉందా అని మేము త్వరగా గుర్తించగలము. Cosθ = (•) / (|||| ||||) తో ప్రారంభించండి:
  • సమీకరణం యొక్క ఎడమ మరియు కుడి వైపులా ఒకే గుర్తు ఉండాలి (సానుకూల లేదా ప్రతికూల).
  • పొడవు ఎల్లప్పుడూ సానుకూలంగా ఉన్నందున, cosθ స్కేలార్ ఉత్పత్తికి సమానమైన చిహ్నాన్ని కలిగి ఉండాలి.
  • అందువల్ల, ఉత్పత్తి సానుకూలంగా ఉంటే, cosθ కూడా సానుకూలంగా ఉంటుంది. మేము unit <π / 2 లేదా 90º తో యూనిట్ సర్కిల్ యొక్క మొదటి క్వాడ్రంట్లో ఉన్నాము. కనుగొనవలసిన కోణం పదునైన కోణం.
  • స్కేలార్ ఉత్పత్తి ప్రతికూలంగా ఉంటే, cosθ ప్రతికూలంగా ఉంటుంది. మేము unit / 2 <π లేదా 90º <θ ≤ 180º తో యూనిట్ సర్కిల్ యొక్క రెండవ క్వాడ్రంట్లో ఉన్నాము. అది జైలు మూలలో ఉంది.